1.
Introduction
In part 1 I explained the software
architecture used for doing transformations between two different coordinates
systems. In this document I will show you how in JavaScript you can develop the
different functions (conversions and translations) needed for the transformations. All the functions showed
here are not related to ArcGis , so you
can use them on all situations when You need to convert local coordinates.
The transformation that will be implemented
here is those between the WGS 84 geographic coordinates systems and the Lambert
72 projected coordinates systems. As you
already seen in part 1, the transformation happens through different steps.
Some of these steps can be used in the transformations of other coordinates
systems than Lambert 72. However some of
the functions used are only valid for the Lambert 72 projected coordinates
systems.
When writing a transformation yourself, you
will need some form of unit testing. This will only partial covered here, but in the document OGP
Publication 373-7 there are test values that can be used with simple function
calls. It is important of doing unit tests on each different function before a
complete integration can be done of the different steps. An error on one of the
steps results in inaccurate coordinates and makes it difficult to debug a wrong
transformation.
2.
Software algorithm outlined
To support different conversions and
translations, two tables of JSON objects
are used. One table defines the ellipsoid parameters and another table defines
the translation parameters, mainly the Helmert 7 parameters.
Below is an example of some values in the tables.
// ellipse
parameters
CoordTransform.ellipse = {GRS80: {
a: 6378137,
b: 6356752.3141,
f: 1 / 298.2572215381486,
e: 0.08181919111988833,
e2: 0.006694380035512838
},
Intl1924: {
a: 6378388.000,
b: 6356911.946,
f: 1 / 296.9999982305938,
e: 0.0819918902228546,
e2: 0.006722670062316669
},
Agd66: {
a: 6378160.0,
b: 6356774.719,
f: 1 / 298.25,
e: 0.08182018036905428,
e2: 0.006694541915624534
},
WGS84: {
a: 6378137,
b: 6356752.3142,
f: 1 / 298.2572229328697,
e: 0.08181919092890624,
e2: 0.006694380004260827
}
};
//
Transformation parameters (Helmert + Conic Conformal SP2 (Belgium)
CoordTransform.datumTransform = {toLambert72: {
tx: 106.868628, ty: -52.297783, tz: 103.723893,
rx: -0.33657, ry: 0.456955, rz: -1.842183,
s: -1.2747,
latF: 1.57079633,
lngF: 0.07604294,
lat1Par: 0.86975574,
lat2Par: 0.89302680,
eastF: 150000.01256,
northF: 5400088.4378
},
fromLambert72: {
tx: -106.868628, ty: 52.297783, tz: -103.723893,
rx: 0.33657, ry: -0.456955, rz: 1.842183,
s: -1.2747,
latF: 1.57079633,
lngF: 0.07604294,
lat1Par: 0.86975574,
lat2Par: 0.89302680,
eastF: 150000.01256,
northF: 5400088.4378
},
toWGS72: {
tx: 0, ty: 0, tz: 4.5,
rx: 0, ry: 0, rz: 0.554,
s: 0.219
},
toAGD66: {
tx: -134, ty: -48, tz: 149,
rx: 0, ry: 0, rz: 0,
s: 1.0
},
fromAGD66: {
tx: 134, ty: 48, tz: -149,
rx: 0, ry: 0, rz: 0,
s: 1.0
}
}
To simplify the functions of translation
using the Helmert 7 parameters, two entries in the table are used, having only
a difference in sign.
3.
Functions used in the
transformation process
This section gives the different functions
that are required in doing transformation between coordinate systems. Not all of these functions are generic for
all transformations but it gives an idea how to create specific
transformations. Some functions depends on the local coordinates system
involved.
3.1 Geographic coordinates to geocentric coordinates
transformation
This method will convert the WGS 84
geographic coordinates into x, y, z geocentric coordinates. The method requires
as input a point expressed in latitude ,longitude and height together with the
ellipsoid. The method returns the
geocentric coordinates x, y, y expressed in meters. This method is generic for
all ellipsoid.
function
geographic2Geocentric(lat, lon, h, e) {
///
<summary>/// Transformation of geographic x,y coordinates to geocentric coordinates
/// </summary>
/// <param name="lat">lat source</param>
/// <param name="lon">lon source</param>
/// <param name="h">hight</param>
/// <param name="e">eclipsoide parameters</param>
/// <returns type="">x,y geocentric coordinates</returns>
var a = e.a, b = e.b, f = e.f;
var sinPhi = Math.sin(lat);
var cosPhi = Math.cos(lat);
var sinLambda = Math.sin(lon);
var cosLambda = Math.cos(lon);
var H = h; // standard hight
var eSq = (a * a - b * b) / (a * a);
var nu = a / Math.sqrt(1 - eSq * sinPhi * sinPhi);
var x1 = (nu + H) * cosPhi * cosLambda;
var y1 = (nu + H) * cosPhi * sinLambda;
var z1 = ((1 - eSq) * nu + H) * sinPhi;
return { x: x1, y: y1, z: z1 }
}
3.2 Geocentric transformation
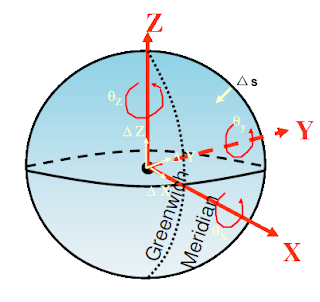
In the figure you can see the different
Helmert 7 parameters consisting of the delta of the origin of the ellipsoid ,
angle of rotation of the axes and a scale factor.
In the case of WGS 84 geographic
coordinates system to Lambert 72 projected coordinates systems I need the
Helmert 7 parameter translation. For other geocentric transformations it is
possible you will need the Molodensky-Badekas 10 parameter translation. Here I will illustrate the Helmert 7
parameter translation. This translation is generic for all transformation that
requires Helmert 7. The Molodensky-Badekas 10 parameter
translation is similar as the Helmert 7, adding some offset based on the extra
three parameters.
The Helmert 7 parameter translation is
mainly a matrix multiplication. Input are the geocentric coordinates x, y, z
and the transformation parameter defined in the supporting table.
function
helmertTransform(point, t) {
///
<summary>
/// Helmert -7
parameter transformations between two elipsoides/// </summary>
/// <param name="point">x,y coordinates of the source</param>
/// <param name="t">transformation with the 7 parameters</param>
/// <returns type="">x,y coordinates</returns>
var tx = t.tx, ty = t.ty, tz = t.tz;
var rx = (t.rx / 3600).toRad(); // normalise seconds to radians
var ry = (t.ry / 3600).toRad();
var rz = (t.rz / 3600).toRad();
var s1 = (t.s / 1e6); // normalise ppm to (s+1)
// apply transform
var x2 = tx + (point.x - point.y * rz + point.z * ry) + s1 * point.x;
var y2 = ty + (point.y + point.x * rz - point.z * rx) + s1 * point.y;
var z2 = tz + (point.z - point.x * ry + point.y * rx) + s1 * point.z;
return { x: x2, y: y2, z: z2 }
}
3.3 Geocentric coordinates to geographic coordinates
This function is needed to transfer
geocentric coordinates back to the geographic coordinates. Geocentric
coordinates cannot been used in displayed on a map, so minimal this
transformation is required for using the result after a transformation. The function required as input geocentric
coordinates x, y, z and the ellipsoid parameters described earlier. The result
of the function is a location expressed in latitude, longitude and height. This
Is not a simple transformation but an iterating formula based on
function
geocentric2Geographic(point, e) {
///
<summary>
/// Transformation
of geocentric coordinates to geographic coordinates/// </summary>
/// <param name="point">x,y,z geocentric coordinates</param>
/// <param name="e">eclipsoid parameters</param>
/// <returns type="">geographic coordinates latitude,longitude,height</returns>
var a = e.a, b = e.b, f = e.f;
var precision = 2 / a;
eSq = (a * a - b * b) / (a * a);
var p = Math.sqrt(point.x * point.x + point.y * point.y);
var lat2 = Math.atan2(point.z, p * (1 - eSq)), phiP = 2 * Math.PI;
while (Math.abs(lat2 - phiP) > precision) {
nu = a / Math.sqrt(1 - eSq * Math.sin(lat2) * Math.sin(lat2));
phiP = lat2;
lat2 = Math.atan2(point.z + eSq * nu * Math.sin(lat2), p);
}
var lng2 = Math.atan2(point.y, point.x);
H = p / Math.cos(lat2) - nu;
// h = X sec λ sec ϕ – ν
var eta = eSq / (1 - eSq);
b = a * (1 - f);
p = Math.sqrt(point.x * point.x + point.y * point.y);
var q = Math.atan2(point.z * a, p * b);
var latSimple =
Math.atan2(point.z + eta * b * Math.sin(q) * Math.sin(q) * Math.sin(q),
p - eSq * a * Math.cos(q) * Math.cos(q) * Math.cos(q));
return { lng: lng2, lat: lat2, h: H };
}
3.4 Lambert Conic Conformal two standard parallel (2SP) (Belgium)
In case of Lambert 72 projected coordinates
system I need a conversion of geographic 3D coordinates into 2D projected
coordinates based on a conic conformal transformation. When using other projected
coordinates system you will need to verify the document OGP Publication 373-7 to
select the formula to be applied. The
function is based on the more generic Lambert Conic Conformal SP2 with a
correction added for Belgium.
function conicConformalSP2(pointLatLng,
e, t) {
///
<summary>
/// Conic
Conformal SP2 transformation of geographic coordinates to Lambert 72 x,y/// with correction for Belgium
/// Is only valid in case of Lambert 72 datum
/// </summary>
/// <param name="pointLatLng">Lambert 72 geographic coordinates</param>
/// <param name="e">Eclipsoid parameters for the datum</param>
/// <param name="t">Translation object containing the parameters</param>
/// <returns type="">x,y parameters of the projection</returns>
// m = [cosϕ/(1 – e²sin²ϕ)] 0.5
var m1 = Math.cos(t.lat1Par) / Math.sqrt((1 - e.e2 * Math.sin(t.lat1Par) * Math.sin(t.lat1Par)));
var m2 = Math.cos(t.lat2Par) / Math.sqrt((1 - e.e2 * Math.sin(t.lat2Par) * Math.sin(t.lat2Par)));
// t = tan(p /4 – ϕ/2)/[(1 – e sinϕ )/(1 + e sinϕ )]e/2
var t1 = Math.tan(Math.PI / 4 - t.lat1Par / 2) / Math.pow((1 - e.e * Math.sin(t.lat1Par)) / (1 + e.e * Math.sin(t.lat1Par)), e.e / 2);
var t2 = Math.tan(Math.PI / 4 - t.lat2Par / 2) / Math.pow((1 - e.e * Math.sin(t.lat2Par)) / (1 + e.e * Math.sin(t.lat2Par)), e.e / 2);
var tF = Math.tan(Math.PI / 4 - t.latF / 2) / Math.pow((1 - e.e * Math.sin(t.latF)) / (1 + e.e * Math.sin(t.latF)), e.e / 2);
if (Math.abs(tF) < 0.0000001)
tF = 0;
var tPt = Math.tan(Math.PI / 4 - pointLatLng.lat / 2) / Math.pow((1 - e.e * Math.sin(pointLatLng.lat)) / (1 + e.e * Math.sin(pointLatLng.lat)), e.e / 2);
// n = (ln m1 – ln m2)/(ln t1 – ln t2)
var n = (Math.log(m1) - Math.log(m2)) / (Math.log(t1) - Math.log(t2));
// F = m1/(nt1ⁿ)
var F = m1 / (n * Math.pow(t1, n));
// r = a F tn
var r = e.a * F * Math.pow(tPt, n);
var rF = 0;
if (tF > 0)
rF = e.a * F * Math.pow(tF, n);
// θ = n(λ – λF)
var tetra = n * (pointLatLng.lng - t.lngF);
var a = 0.00014204313635987700;
var x = t.eastF + r * Math.sin(tetra - a);
var y = t.northF + rF - r * Math.cos(tetra - a);
return { x: x, y: y };
}
3.5 Putting all the different steps together
In the previous sections the different
steps needed for the transformation has been explained. Having developed these
different steps, I now have the possibility to do the transformation into one
function. As the name of the function suggests, this is only applicable between
WGS 84 coordinates system and Lambert 72 projected coordinates system. Test
done on the transformation results reveals an accuracy of 10 centimeters in x
and y coordinates.
function
convertWGS84toLambert72(pWGS84) {
///
<summary>
/// Convert
lat/lon point in WGS84 to Lambert 72 x,y projection coordinates/// </summary>
/// <param name="pWGS84"> WGS84 geographic lat/lon in degrees</param>
/// <returns type="x,y">Lambert 72 projection x,y </returns>
var eWGS84 = CoordTransform.ellipse.GRS80;
var eIntl1924 = CoordTransform.ellipse.Intl1924;
var txToLambert72 = CoordTransform.datumTransform.toLambert72;
var pLambert72h = convertEllipsoid(pWGS84, eWGS84, txToLambert72, eIntl1924);
// Convert lat lng towards X, Y in lambert 72
var pointXY = conicConformalSP2(pLambert72h, eIntl1924, txToLambert72);
return pointXY;
}
function
convertEllipsoid(point, e1, t, e2) {
/// <summary>
/// Convert lat/lon from one ellipsoidal model to another
/// </summary>
/// <param name="point">lat/lng in source datum</param>
/// <param name="e1">source ellipsoide parameters</param>
/// <param name="t">Helmert 7 transform parameters</param>
/// <param name="e2">target ellipsoide parameters</param>
/// <returns type="">lat/lon in target reference datum</returns>
// -- 1: convert polar to cartesian coordinates (using ellipse 1)
var lat = point.lat * (Math.PI / 180.0);
var lon = point.lng * (Math.PI / 180.0);
var point1 = geographic2Geocentric(lat, lon, 100, e1);
// -- 2: apply helmert transform using appropriate params
var point2 = helmertTransform(point1, t)
// -- 3: convert cartesian to polar coordinates (ellipse 2) browring algorithm
var pointLatLng = geocentric2Geographic(point2, e2);
return pointLatLng;
}
4.
Creating another type of transformation
In the previous section we put all the
functions together to have our transformation from WGS84 coordinates system to
Lambert 72 projected coordinates system. Now I will illustrate how we can use
the same function to go the other way in the transformation. I will now show
you how we can make a transformation of Lambert 72 projected system to the WGS
84 coordinate system. The following figure illustrate how this must be done.
From the different steps described here for
doing the transformation, we only misses the code for doing the transformation
‘Projected 2D to 3D geographic’ for Lambert 72 coordinate system. We need to do
a transformation similar as described in
section 6 but now the other way. In our famous document OGP Publication 373-7 you can find the formula needed for doing
this.
4.1 Reverse Lambert
Conic Conformal 2SP (Belgium)
For each transformation geographic 2D
coordinates to projected 3D coordinates there exist a reverse formula.
Hereafter you can find the reverse formula for the Lambert Conic Conformal 2SP.
For Belgium we needs also a slightly modified version to perform a correction.
function
conicConformalSP2Reverse(pointxy, e, t) {
///
<summary>
/// Reverse Conic
Conformal SP2 (Belgium) transformation of Lambert 72 x,y to /// geographic coordinates
/// </summary>
/// <param name="pointxy">x,y,h Lambert 72 projections</param>
/// <param name="e">Eclipsoid parameters for the datum</param>
/// <param name="t">Translation object containing the parameters</param>
/// <returns type="">Geographic coordinates lat/Lng</returns>
var m1 = Math.cos(t.lat1Par) / Math.sqrt((1 - e.e2 * Math.sin(t.lat1Par) * Math.sin(t.lat1Par)));
var m2 = Math.cos(t.lat2Par) / Math.sqrt((1 - e.e2 * Math.sin(t.lat2Par) * Math.sin(t.lat2Par)));
// t = tan(p /4 – ϕ/2)/[(1 – e sinϕ )/(1 + e sinϕ )]e/2
var t1 = Math.tan(Math.PI / 4 - t.lat1Par / 2) / Math.pow((1 - e.e * Math.sin(t.lat1Par)) / (1 + e.e * Math.sin(t.lat1Par)), e.e / 2);
var t2 = Math.tan(Math.PI / 4 - t.lat2Par / 2) / Math.pow((1 - e.e * Math.sin(t.lat2Par)) / (1 + e.e * Math.sin(t.lat2Par)), e.e / 2);
var tF = Math.tan(Math.PI / 4 - t.latF / 2) / Math.pow((1 - e.e * Math.sin(t.latF)) / (1 + e.e * Math.sin(t.latF)), e.e / 2);
if (Math.abs(tF) < 0.0000001)
tF = 0;
// n = (ln m1 – ln m2)/(ln t1 – ln t2)
var n = (Math.log(m1) - Math.log(m2)) / (Math.log(t1) - Math.log(t2));
// F = m1/(nt1ⁿ)
var F = m1 / (n * Math.pow(t1, n));
var rF = 0;
if (tF > 0)
rF = e.a * F * Math.pow(tF, n);
var r = Math.sqrt(Math.pow((pointxy.x - t.eastF), 2) + Math.pow(rF - (pointxy.y - t.northF), 2));
var tbis = Math.pow(r / (e.a * F), 1 / n);
var tetra = Math.atan((pointxy.x - t.eastF) / (rF - (pointxy.y - t.northF)));
var precision = 0.0000000001;
// ϕ = π/2-2atan t'.
var lat2 = Math.PI / 2 - 2 * Math.atan(tbis);
var lat = 0;
while (Math.abs(lat - lat2) > precision) {
lat = lat2;
lat2 = Math.PI / 2 - 2 * Math.atan(tbis * Math.pow((1 - e.e * Math.sin(lat)) / (1 + e.e * Math.sin(lat)), e.e / 2));
}
// λ = [(θ' + a)/n] + λF
lng = (tetra + (29.2985 / 3600).toRad()) / n + t.lngF;
lat2 = lat2 * 180 / Math.PI;
lng = lng * 180 / Math.PI;
return { lat: lat2, lng: lng, h: 100 }
}
More details how these function is build
can be found in OGP Publication 373-7
4.2 Creating the
full transformation
This is similar as the function described
in section 7. The only difference is that we now has to add an initial
transformation between projected coordinates and geographic coordinates.
function convertLambert72toWGS84(pLambert)
{
///
<summary>
/// Convert x,y,h
point in Lambert 72 projection to WGS84 geographic coordinates/// </summary>
/// <param name="pLambert">x,y Lambert projection</param>
/// <returns type="">WGS84 geographic Lat,Lng in degrees</returns>
var eWGS84 = CoordTransform.ellipse.GRS80;
var eIntl1924 = CoordTransform.ellipse.Intl1924;
var txFromLambert72 = CoordTransform.datumTransform.fromLambert72;
var pointLatLng = conicConformalSP2Reverse(pLambert, eIntl1924, txFromLambert72);
var pLatLng = convertEllipsoid(pointLatLng, eIntl1924, txFromLambert72, eWGS84);
pLatLng.lat = pLatLng.lat * 180 / Math.PI;
pLatLng.lng = pLatLng.lng * 180 / Math.PI;
return pLatLng;
}
5.
Conclusion
This illustrate how both transformation can
be achieved with the same functions. In this way an important part of the
functions are reusable across different transformations. In the JavaScript
implementations of the formula’s no care was done to optimize the code but
rather make it readable towards the formulas found in OGP Publication 373-7.
6.
Testing
An important part for writing your own
transformation between two coordinates systems is creating test procedures.
Before you can write test procedures, you will need having test data. Important
data can be found in the document OGP Publication 373-7.
Sometimes you can find sample data on the internet. In Belgium we
have the desktop utility cConvert of NGI (Nationaal Geografisch Instituut) that
make it possible to convert coordinates
between WGS 84 and different Belgium projected coordinates systems.Here are some examples of writing test procedure. The conversion of geographic to geocentric coordinates can be tested using a bidirectional conversion :
var pointLatLngInit = {
lat: 0.939151102,lng: 0.037167659,
h: 100
};
var pointXY =
geographic2Geocentric(pointLatLngInit.lat, pointLatLngInit.lng,
pointLatLngInit.h,
CoordTransform.ellipse.GRS80);// Geodetic coordinates x,y,z after geographic2Geocentric
// 3771793.968, 140253.342, 5124304.349
pointLatLng = geocentric2Geographic(pointXY, CoordTransform.ellipse.GRS80);
var dif = Math.abs(pointLatLng.lat - pointLatLngInit.lat) +
Math.abs(pointLatLng.lng - pointLatLngInit.lng);
// Must be 0.939151102, 0.037167659
if (dif > 0.00001)
alert("Error occurred during the geographic - geocentric transformation");
For testing the Helmet 7 parameter
translation you can test it with given data as a first test. This is what is
shown next.
var point = { x:
3657660.66, y: 255768.55, z: 5201382.11 };
var pointCentric =
helmertTransform(point, CoordTransform.datumTransform.toWGS72);// XT = 3657660.78 m
// YT = 255778.43 m
// ZT = 5201387.75 m
However a more extensive can be done using a
bidirectional tests doing a conversion between two geographic coordinates
systems. This is illustrated in the code
hereafter.
// WGS84 :
50.679013094° 5.808676779°
// WGS84 - Lambert
72 transformation var pointLatLngInit = { lat: 50.679013094, lng: 5.808676779, h: 100 };
pointLatLng2 = convertEllipsoid(pointLatLngInit, CoordTransform.ellipse.GRS80, CoordTransform.datumTransform.toLambert72, CoordTransform.ellipse.Intl1924);
pointLatLng2.lat = pointLatLng2.lat * 180 / Math.PI;
pointLatLng2.lng = pointLatLng2.lng * 180 / Math.PI;
// Lambert 72 : 50.679571311° 5.807373188°
pointLatLng = convertEllipsoid(pointLatLng2, CoordTransform.ellipse.Intl1924,
CoordTransform.datumTransform.fromLambert72, CoordTransform.ellipse.GRS80);
//
pointLatLng.lat = pointLatLng.lat * 180 / Math.PI;
pointLatLng.lng = pointLatLng.lng * 180 / Math.PI;
// WGS84 : 50.679013094° 5.808676779°
var dif = Math.abs(pointLatLng.lat - pointLatLngInit.lat) +
Math.abs(pointLatLng.lng - pointLatLngInit.lng);
if (dif > 0.00001)
alert("Error occurred during the geographic - geographic transformation");
For some geographic transformations you can
use the Abridged Molodensky formula. This is a transformation based on only
three parameters , DX, DY, DZ.
// Abridged
Molodensky transformations
var pointLatLngInit = {
lat: -37.8, lng: 144.96666667, h: 50 };
var pointLatLng2 = molodenskyTransform(pointLatLngInit, CoordTransform.datumTransform.toAGD66,
CoordTransform.ellipse.Agd66, CoordTransform.ellipse.GRS80);
// Results -37.79848036 144.96798611 46.378
// -0.659707935 2.530168668
pointLatLng2.lat = pointLatLng2.lat * 180 / Math.PI;
pointLatLng2.lng = pointLatLng2.lng * 180 / Math.PI;
var pointLatLng =
molodenskyTransform(pointLatLng2, CoordTransform.datumTransform.fromAGD66,
CoordTransform.ellipse.GRS80, CoordTransform.ellipse.Agd66);
pointLatLng.lat = pointLatLng.lat * 180 / Math.PI;
pointLatLng.lng = pointLatLng.lng * 180 / Math.PI;
var dif = Math.abs(pointLatLng.lat - pointLatLngInit.lat) +
Math.abs(pointLatLng.lng - pointLatLngInit.lng);
if (dif > 0.000001)
alert("Error occurred during the geographic-geographic molodensky transformation");
Above test procedure is based on a
transformation between geographic coordinates system of Great Britain and WGS
84. As in a previous test procedure, it can also been used in bidirectional
calls.
For doing this test You need the Abridge Molodensky formula function implementation. Only three
parameters are required for this transformation.
function
molodenskyTransform(point, t, eFrom, eTo) {
///
<summary>
/// Molodensky
transformation between geografic coordinates of two eclipsoides/// </summary>
/// <param name="point">lat,lng of source</param>
/// <param name="t">transformation between the eclipsoides</param>
/// <param name="eFrom">eclipsoide parameters of source</param>
/// <param name="eTo">eclipsoide parameters of destination</param>
/// <returns type="">lat,lng transformed</returns>
var lat = point.lat * Math.PI / 180;
var lng = point.lng * Math.PI / 180;
var da = eTo.a - eFrom.a;
var df = eTo.f - eFrom.f;
var sinLat = Math.sin(lat);
var cosLat = Math.cos(lat);
var sinLng = Math.sin(lng);
var cosLng = Math.cos(lng);
var sin2Lat = sinLat * sinLat;
var esqr = eFrom.f * (2 - eFrom.f);
var nu = eFrom.a / Math.sqrt(1 - esqr * sin2Lat);
var ro = eFrom.a * (1.0 - esqr) / Math.pow((1.0 - esqr * sin2Lat), 1.5);
var dlat = (1 / (ro + point.h)) * (-t.tx * sinLat * cosLng - t.ty * sinLat * sinLng
+ t.tz * cosLat + da * (nu * esqr * sinLat * cosLat) / eFrom.a
+ sinLat * cosLat * df * ((ro / (1 - eFrom.f)) + nu * (1 - eFrom.f)));
var dlng = (-t.tx * sinLng + t.ty * cosLng) / ((nu + point.h) * cosLat);
var dh = t.tx * cosLat * cosLng + t.ty * cosLat * sinLng + t.tz * sinLat - da +
sin2Lat * (eFrom.f * da + eFrom.a * df);
return { lat: lat + dlat, lng: lng + dlng, h: point.h + dh };
}
7.
Possible extensions
In the transformation function illustrated
here, no action is implemented to handle spatial distortion. Although you can
find on the documents of the bibliography in part 1 some formula’s that will
handle this distortion like Tissot, it is possible that at country level
specific translation is put in place. This kind of correction is only needed if
you need an accuracy of centimeters.
Example of such a situation is Belgium
where NGI has defined regions, which each region has its own Helmet 7
parameters.
Some examples.
|
zone
|
dx
|
dy
|
dz
|
rx
|
ry
|
rz
|
s
|
|
zone01
|
170,194330
|
-23,319088
|
98,006431
|
-0,132903
|
1,272427
|
2,691469
|
0,999995501
|
|
zone02
|
154,854804
|
-24,618147
|
65,952209
|
0,006332
|
1,547517
|
2,851635
|
1,000000934
|
|
zone03
|
168,604000
|
-19,720000
|
59,218000
|
-0,036000
|
2,036000
|
3,046000
|
1,000000373
|
|
zone04
|
153,029709
|
-18,859783
|
84,124233
|
0,022832
|
1,137474
|
3,146639
|
0,999998870
|
|
zone05
|
158,041429
|
-15,912627
|
73,921469
|
-0,094578
|
1,470761
|
3,161524
|
0,999999603
|
|
zone06
|
135,404412
|
-13,372664
|
82,710991
|
-0,146833
|
0,722672
|
3,241832
|
1,000000767
|
|
zone07
|
148,388053
|
0,104964
|
86,472784
|
-0,256388
|
0,983121
|
3,778806
|
0,999998948
|
|
zone08
|
158,411443
|
-15,389660
|
67,316637
|
0,206397
|
1,632895
|
3,568474
|
1,000000369
|
|
zone09
|
168,285000
|
-18,249000
|
63,917000
|
0,027082
|
1,936736
|
3,194554
|
0,999999823
|
|
zone10
|
155,950000
|
-19,541000
|
71,852000
|
0,031006
|
1,462467
|
3,136918
|
1,000000081
|


